It's that time of year again when many people are deciding which college they should attend come fall. Whether they are a high school senior, aspiring professional, or seasoned veteran seeking an MBA, the ultimate decision of which college is based largely on reputation.The perennial data source for college ratings that most students turn to is the US News America's Best Colleges Rankings. Despite the limited usefulness of reading rankings, there is only so much information you can get from first-hand experience. Taking the campus tour, talking with students and doing your own due diligence is about as far as you can go short of attending the school. The US News ranking methodology is based on many factors: peer assessment, faculty resources, selectivity, class sizes, and financial aid, among many others. What does it really mean to rank a list of schools? I can define a personal value function for determining which school I prefer to and by doing pairwise comparisons, I can sort a list of schools based on which would be the most beneficial to my personal goals. However, you can imagine though that an integration of these value functions over a large sample of students would pretty quickly create a ranking distribution that was rather flat. While the US News Rankings strive to give a complete overall view of the school, there are few weaknesses to its method. Some of these weaknesses have stirred criticism for the rankings by both students and colleges.
First, many of the metrics are subjective, such as peer assessment and selectively. This allows for "smoothing out" of the rankings to what the editors expect by "reinterpreting" the selectivity.
My major problem with the US News rankings, however, is that they are not free. In fact, only the top few schools rankings are viewable. Too see the whole list you have to pay $14.95.
So, to this end, I've decided to try my hand at generating my own rankings. Since I'm no expert in the field of evaluating colleges, I'm going to cheat and use statistical learning techniques. I'm going to do this with the help of just Google and some open source software. You won't even have to pay $14.95 to see the results!
First off, I found a list of American Universities from the Open Directory. I parsed out this page with a quick hand-written wrapper to get the names and URLs. Now, the fun part. What kind of "features" should I use for evaluating each school? This is where a bit of editorial control comes to bear. I wanted to capture the essence of what the US News methodology used, but I wanted to do this in a completely automated way using Google. So for each feature, I defined a Google Search query (shown in brackets) that would give me a rough approximation of that particular attribute:
- Peer assessment [link:www.stanford.edu] - This is how some search engines approximate "peer assessment", by counting the number of other pages citing you
- Size [site:www.stanford.edu] - a larger school would have a larger web, right? =)
- Number of faculty [dr. "home page" site:www.stanford.edu] - hopefully those professors have websites that mention "dr." and "home page"
- Scholarly Publications["Stanford University" in scholar.google.com]
- News mentions ["Stanford University" in news.google.com]
First, I load the data into WEKA, a free, open source data mining software package in Java. It implements many off-the-shelf classification and regression algorithms with an API and GUI interface. Let's take a look at few slices of the data:
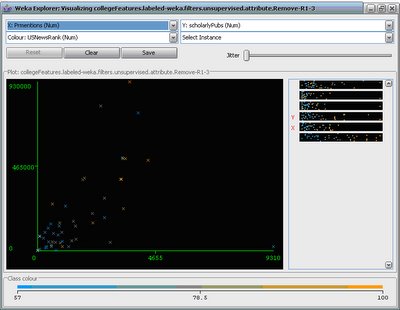This figure plots newsMentions on the x-axis against scholarlyPublications on the y-axis. The points that are plotted are those 50 schools that have a score in the US News rankings (schools beyond the 50th place don't have an overall score in the US News rankings). The color of the dots goes from low(blue) to high(orange). The color trend is blue in the lower-left to orange in the upper-right. As you can see, not only are the two Google queries correllated, they seem to also be jointly correlated to the US News score.
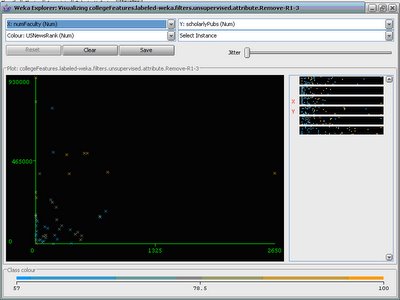Plotting numberFaculty against scholarlyPublications shows also a positive correlation. So maybe these queries weren't totally bogus and have some informational content.The next step is to fit a statistical model to the training data. The basic idea is to train the model on the 50 colleges with USNews scores and to test the model on all 1700+ American colleges. The natural first step is to try to fit a 5-dimensional line through the space. The best fit line is
USNewsRank = (-0.0003)peerAssessment+(0)sizeWeb+(0.0063)numFaculty+(0)scholarlyPubs +This simple model has a root mean squared error(RMSE) of 10.4223. So, in the linear model the size of the web and number of scholarly Publications don't play a role. Fair enough, but can we do better?
0.0002 * newsMentions+68.7534.
The answer is yes. I next used a support vector machine model with a quadratic kernel function. This gave me a RMSE of 7.2724 on the training data. The quadratic kernel allows for more complex dependencies in the training data to be modelled, which is why the training error is lower, but would this result in better evaluation on the larger data set? There is no quick answer to this, but we can see from the ouput what the model predicted.
Name USNews SVM University of Washington 57.4 98.929 Yale University 98 98.081 Harvard University 98 97.953 Massachusetts Institute of Technology 93 92.996 Stanford University 93 92.922 National University 92.523 Columbia University 86 92.255 Princeton University 100 90.609 New York University 65 85.271 University of Chicago 85 85.052 Indiana University 83.973 University of Pennsylvania 93 83.91 Duke University 93 79.487 University of Southern California 66 78.645 University of Pittsburgh 78.274 Cornell University 84 78.051 University of Florida 77.864 University of Colorado 76.877 The American College 76.597 University of California, Berkeley 78 76.192
This table shows the top 20 scores given by my program, along side the US News rating, when available(i.e. when the school was in the top 50). As you can see, many schools recieved consistent marks across the two ratings. However, there are quite a few surprises. My program ranked University of Washington as the best school, where it was only ranked 57.4 by US News. Having visited UDub myself while I was working at Microsoft, I'm not completely surprised. It's a truly modern university that has recently been producing lots of good work--but let's not overgeneralize. I believe that "National University" being high in my rankings is a flaw in the methodology.There are probably many spurious matches to that query like, "Korea National University". Ditto for, "The American College". They just had fortunate names. However, I think the scores for other schools that were unranked by US News like University of Pittsburgh and Indiana University are legitimate.
Now, is this a "good" ranking?It's hard to say since there is no magic gold standard to compare it too. That is the problem with many machine learning experimental designs. But without squabbling too much over the details, I think this quick test shows that even some very basic statistics derived from Google queries can be rich enough in information that they can be used to answer loosely-defined questions. Although I don't think my program is going to have high school guidance counselers worried about their jobs anytime soon, it does do a decent job. An advantage of this approach is that it can be personalized with a few training examples to rank all of the schools based on your own preferences.
Extracting useful knowledge by applying statistics to summary data(page counts) is one thing, but I've taken it to the next level by actually analyzing the stuff within the HTML page. The result of that work is a project called Diffbot, and you can check it out here.
If you're interested, take a look at the full ranking of all 1720 schools(in zipped CSV format).
Now, is this a "good" ranking?It's hard to say since there is no magic gold standard to compare it too. That is the problem with many machine learning experimental designs. But without squabbling too much over the details, I think this quick test shows that even some very basic statistics derived from Google queries can be rich enough in information that they can be used to answer loosely-defined questions. Although I don't think my program is going to have high school guidance counselers worried about their jobs anytime soon, it does do a decent job. An advantage of this approach is that it can be personalized with a few training examples to rank all of the schools based on your own preferences.
Extracting useful knowledge by applying statistics to summary data(page counts) is one thing, but I've taken it to the next level by actually analyzing the stuff within the HTML page. The result of that work is a project called Diffbot, and you can check it out here.
If you're interested, take a look at the full ranking of all 1720 schools(in zipped CSV format).
